Nel primo blocco [1-9] presentiamo le definizioni che servono per delineare la teoria dell'integrazione secondo Riemann,. Vediamo come usare gli integrali per calcolare l'area sottesa dal grafico di una funzione su un intervallo e il volume dei solidi di rotazione. Per concludere trattiamo la teoria degli integrali impropri [27-32]. Ne diamo.. Integrale di (). Area sottesa dal grafico dalla funzione () nel dominio [,]. Si assume che l'area abbia valore negativo quando () è negativa.. In analisi matematica, l'integrale è un operatore lineare che, nel caso di una funzione di una sola variabile a valori reali non negativi, associa alla funzione l'area sottesa dal suo grafico entro un dato intervallo [,] nel dominio.

Calcolo delle aree con gli integrali definiti YouTube

Tabella degli integrali immediati Studenti.it

Integrali dalla A alla Z Gli integrali 1Gli integrali indefiniti 1Prime definizioni

Formulario integrali definiti Studenti.it
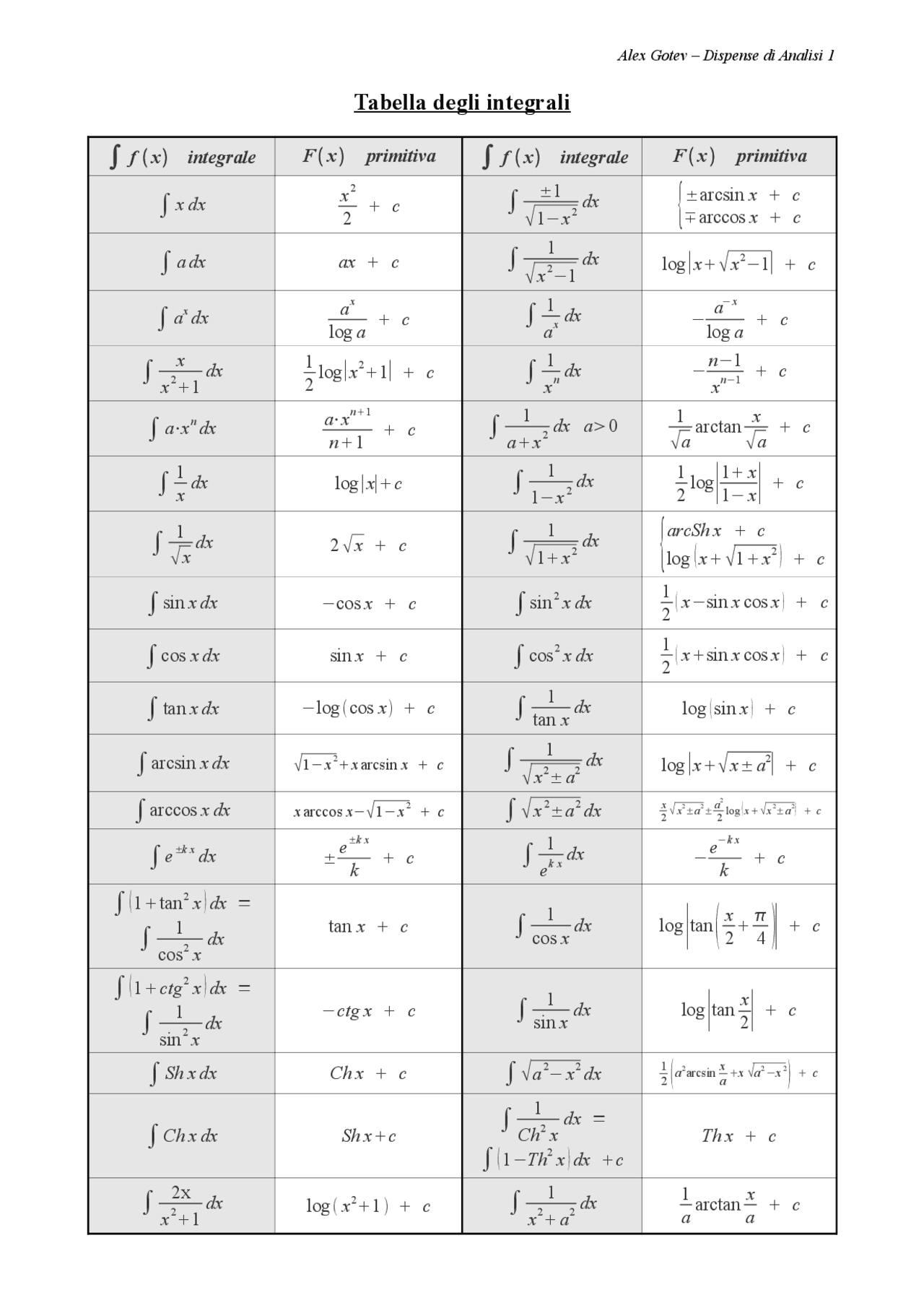
Tabella degli Integrali Docsity

Tabella integrali fondamentali Studenti.it

Tabella integrali fondamentali Studenti.it

Tabella integrali fondamentali Studenti.it
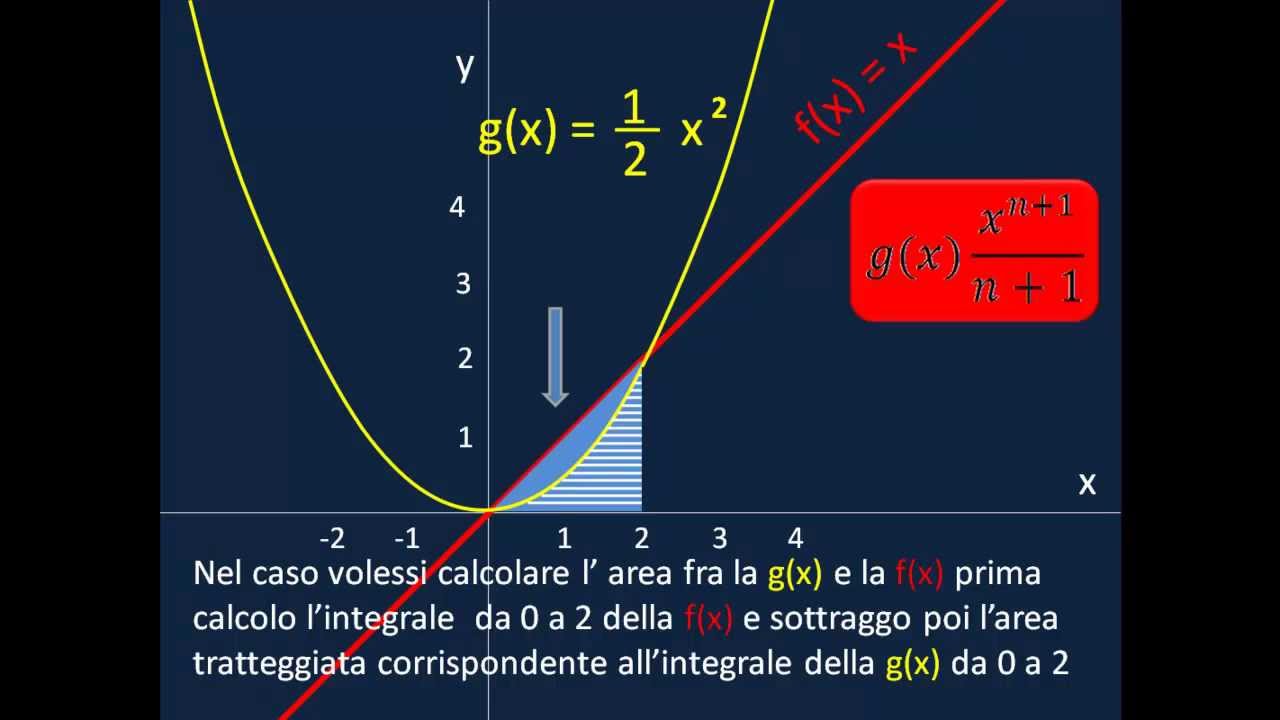
INTEGRALI COSA SONO 1 YouTube

Tabella degli integrali immediati Studenti.it

Come calcolare gli integrali immediati YouTube

Cosa sono gli integrali definiti? Definizione ed esempi

Formulario integrali definiti Studenti.it

Gli integrali indefiniti Matematica Rai Scuola

Integrali Esercizi svolti sugli integrali indefiniti Blog di matematica insieme

Teoremi e calcolo dell'integrale definito per Superiori Redooc

COSA SONO GLI INTEGRALI DEFINITI E CHE RAPPORTO HANNO CON GLI INTEGRALI INDEFINITI YouTube

Tabelle proprietà integrale definito Studenti.it

INTEGRALI TRIPLI cosa sono e a cosa servono YouTube

Integrali di funzioni esponenziali Esercizi (parte 1) YouTube
L'integrale è uno di quei concetti fondamentali della matematica spesso poco compresi dagli studenti delle scuole superiori, ma che ha una vasta gamma di applicazioni nella scienza e nell'ingegneria. In questo articolo, esploreremo a che cosa serve l'integrale e perché è importante nella matematica e nella vita quotidiana. L'integrale è un concetto che si riferisce alla quantità.. Cosa sono gli integrali di superficie. La definizione di integrale di superficie richiede un po' di ingredienti e un po' di requisiti teorici. Vediamoli: • , , una superficie parametrizzata S = r (D) contenuta in R^3 che sia regolare e limitata. Osserviamo che r:D ⊂ R^2 → S è la parametrizzazione della superficie definita su insieme.