Calcolatore gratuito del polinomio caratteristico della matrice - trova il polinomio caratteristico di una matrice passo dopo passo. Polinomio caratteristico. Lo stesso argomento in dettaglio: Polinomio caratteristico e Teorema di diagonalizzabilità. Un modo per verificare che una applicazione è diagonalizzabile è quello di studiare la diagonalizzabilità della sua matrice associata nelle basi degli insiemi di partenza e di arrivo.

Calcolare il Rango di una Matrice YouTube

Determinante di una matrice calcolare il determinante di qualsiasi matrice con una sola

Studio di una funzione e polinomio di Taylor GeoGebra

Trasposta di una Matrice Come si calcola? (con Esercizi Svolti) YouTube
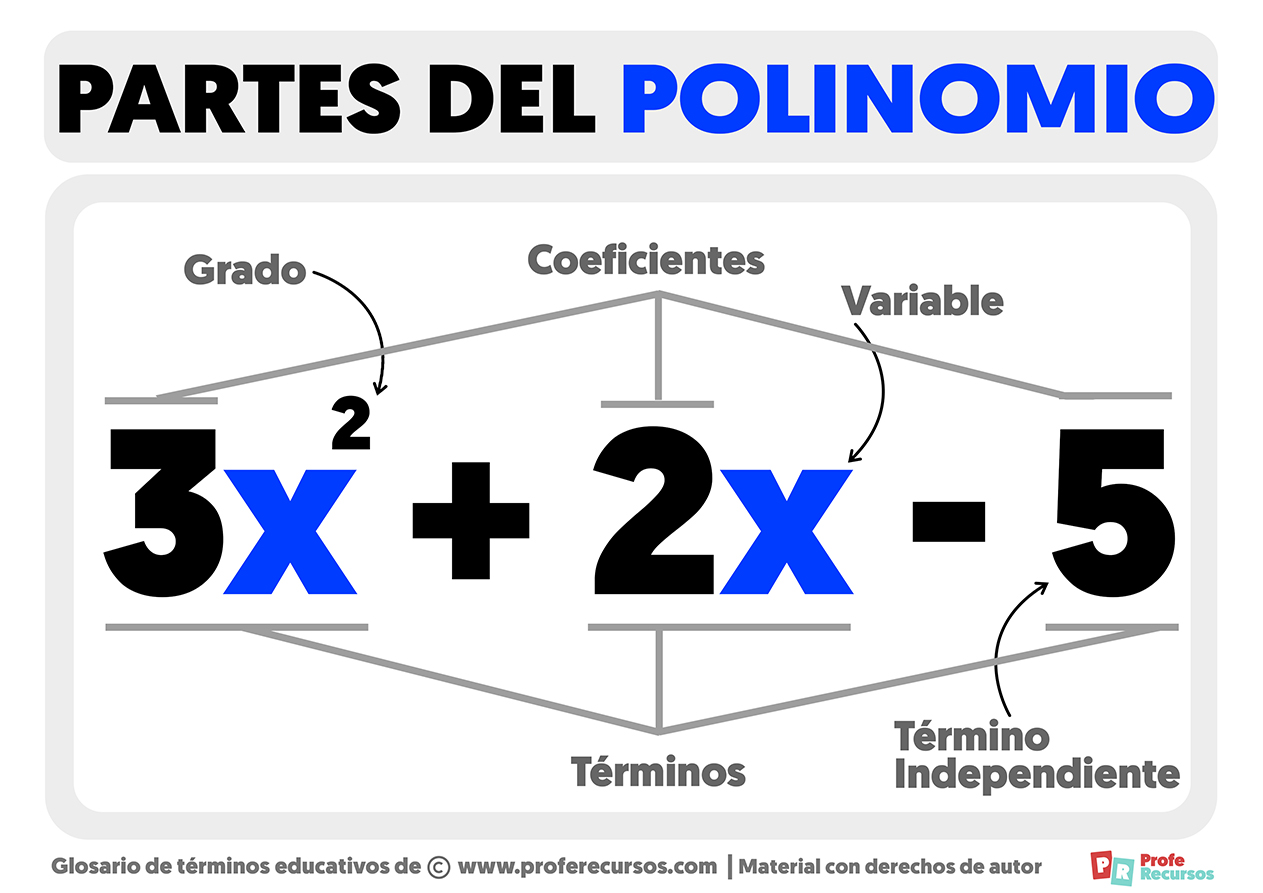
Partes del Polinomio

Algoritmi di diagonalizzazione ppt scaricare

Il determinante di una matrice quadrata incipit Andrea il Matematico

Polinomio caratteristico che significa? Qual è lo

Determinante di una matrice 4x4 Andrea il Matematico

Rango di una matrice calcolare il rango rapidamente .Teoria ed esempi . YouTube
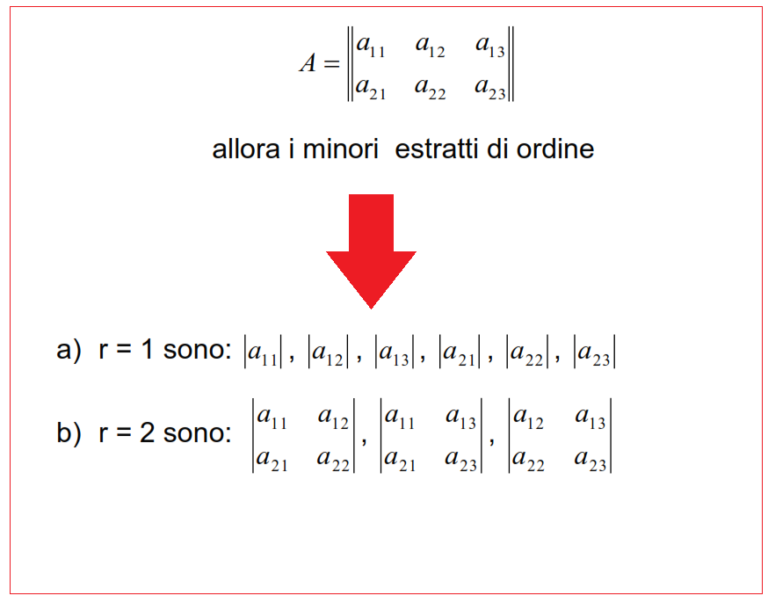
Il rango di una matrice matematica & oltre
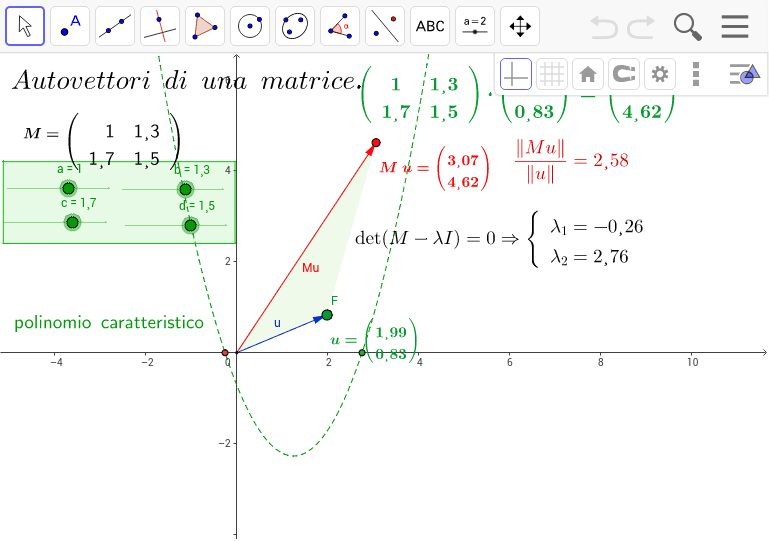
Autovettori di una matrice con polinomio caratteristico GeoGebra
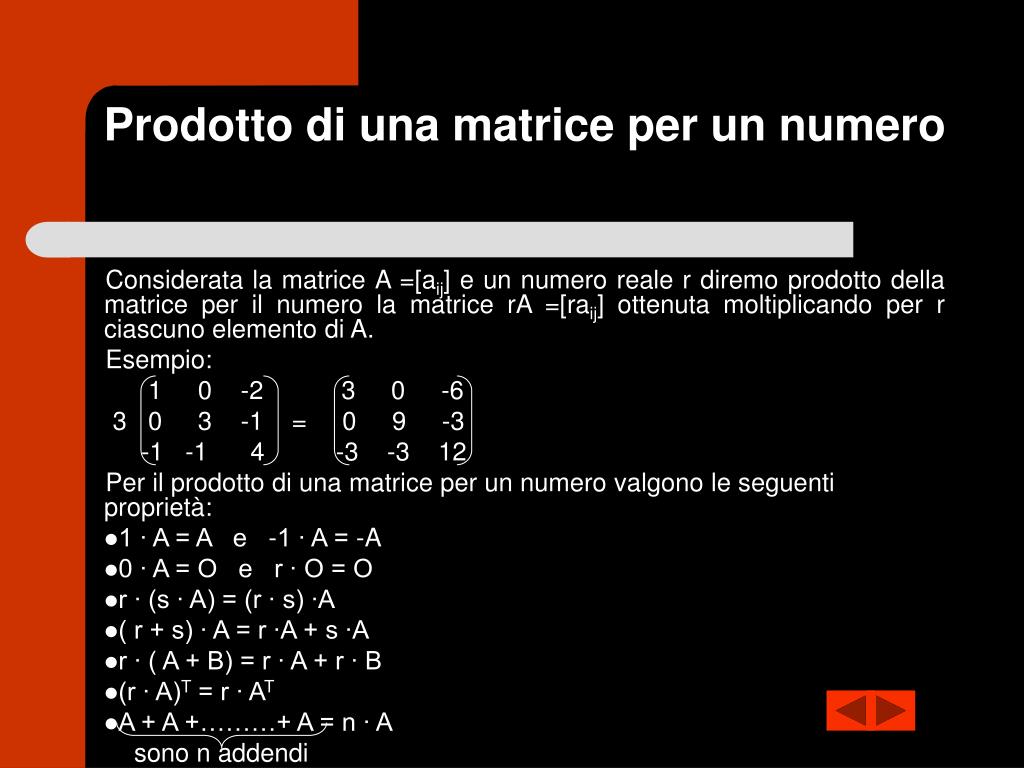
PPT Matrici PowerPoint Presentation, free download ID5027289
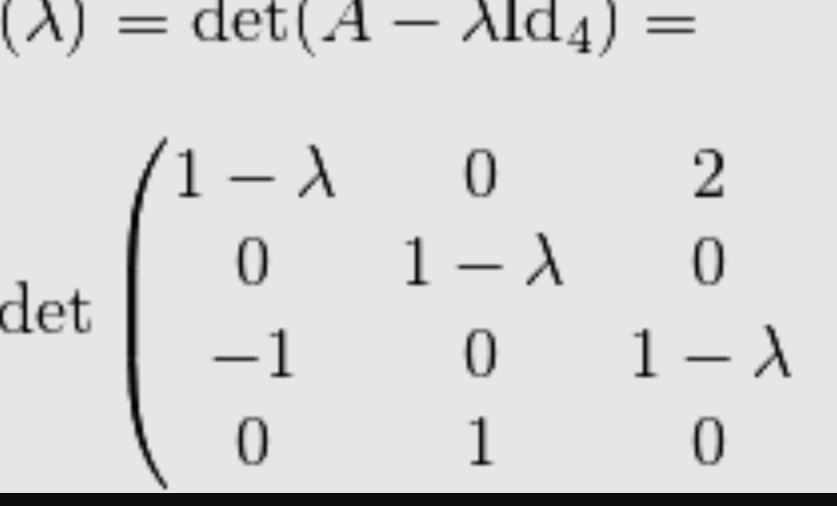
Polinomio caratteristico che significa? Qual è lo

Formula determinante matrice 3x3, matrice 2x2 e matrice 1x1 Studenti.it

DETERMINANTE DI UNA MATRICE 2X2 YouTube

Esercitazioni con Soluzioni, Rango di una matrice Esercizi 9 Rango di una matrice, sistemi

OPERAZIONI CON LE MATRICI Andrea il Matematico

METODO DI SARRUS DETERMINANTE DI UNA MATRICE 3X3 YouTube

POLINOMIO moltiplicazione di polinomio X monomio YouTube
Il polinomio caratteristico è un oggetto che dipende solo dalla classe di similitudine di una matrice, e pertanto fornisce molte informazioni sulla natura intrinseca delle trasformazioni lineari, caratterizzate attraverso la traccia e il determinante.. polinomio caratteristico di una data matrice quadrata A, di ordine n, a elementi in un campo K è il polinomio, di grado n, p A (λ) = det(A − λI), essendo I la matrice identica di ordine n. Gli zeri del polinomio caratteristico, cioè le soluzioni dell'equazione det(A − λI) = 0, sono gli autovalori dell'applicazione lineare.