Introducción En esta entrada definiremos la continuidad de una función, es probable que hayas estudiado antes tal concepto y la manera en que se suele definir de forma intuitiva es mediante la siguiente sentencia: «Si puedes dibujar la función sin levantar el lápiz, entonces es una función continua». Nosotros revisaremos el tema con mayor formalidad, […]. Los límites describen el comportamiento de una función conforme nos acercamos a cierto valor de entrada, sin importar el valor de salida de la función. La continuidad requiere que el comportamiento de una función alrededor de un punto sea igual al valor de la función en ese punto. Esta simple pero poderosa idea juega un papel fundamental en todo el cálculo.

LÍMITE y CONTINUIDAD en FUNCIONES de VARIAS VARIABLES CÁLCULO MULTIVARIABLE YouTube
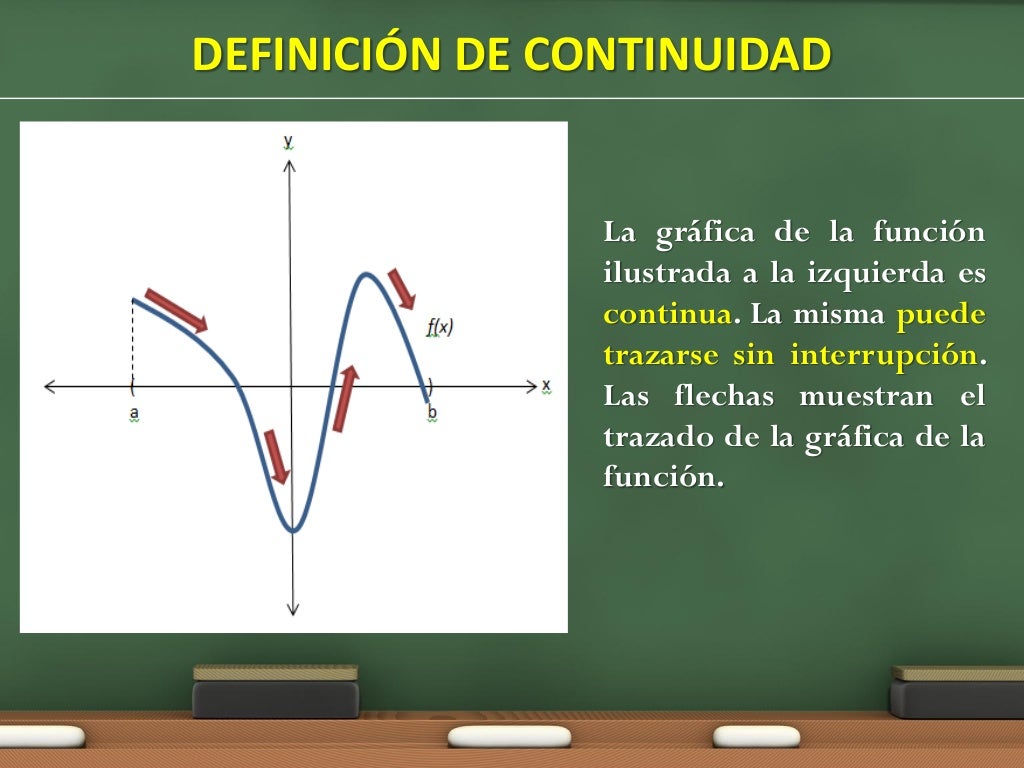
Continuidad (Cálculo I)
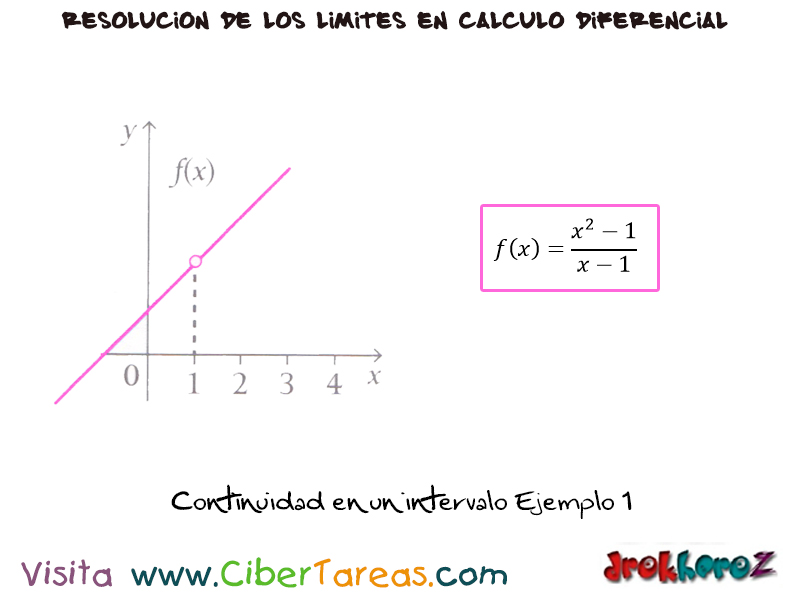
Continuidad en los Límites Cálculo Diferencial CiberTareas

Demostrar continuidad y diferenciabilidad algebraicamente Cálculo Khan Academy en Español

Continuidad de una función Ejemplo 3 YouTube
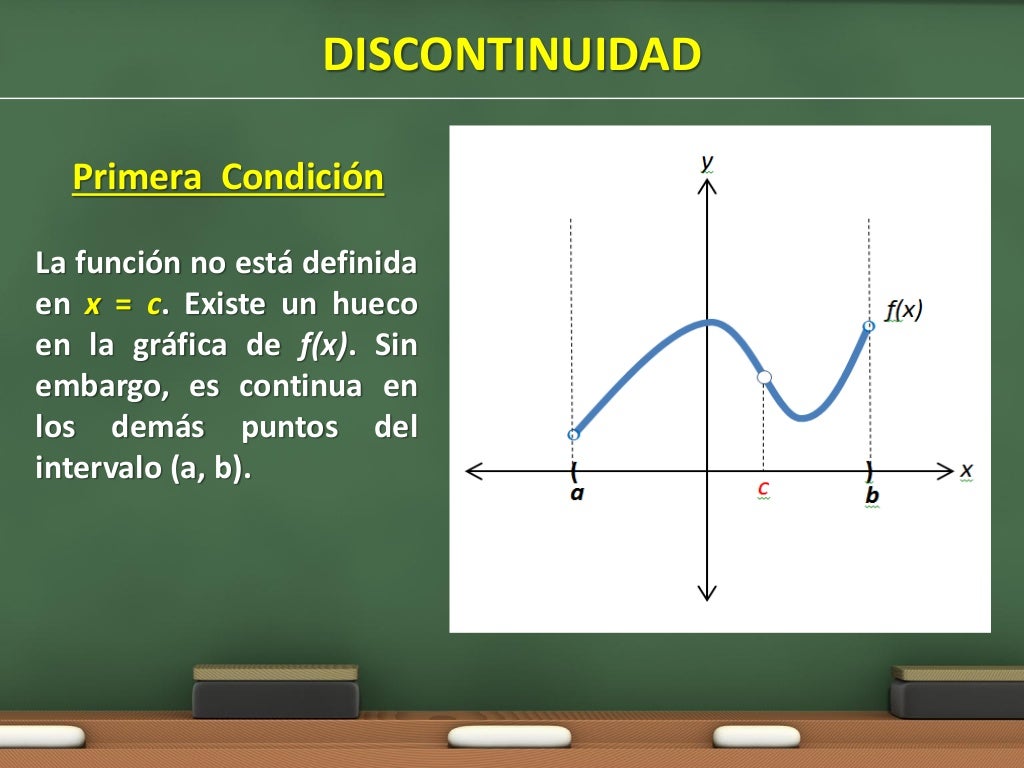
Continuidad (Cálculo I)

Análisis de continuidad de una función YouTube

Continuidad en un punto AP Cálculo AB Khan Academy en Español YouTube
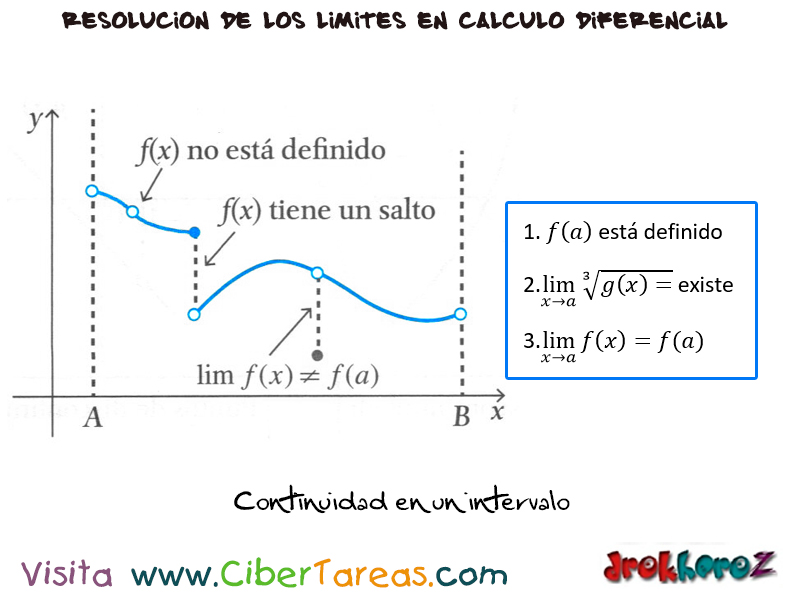
Continuidad en los Límites Cálculo Diferencial CiberTareas

Cálculo Diferencial Continuidad 10 YouTube

Continuidaddiscontinuidad y limites de una funcion

Continuidad de una función Continuidad en un punto YouTube

Continuidad de una función Ejercicio 4 YouTube

Cálculo Vectorial Continuidad YouTube
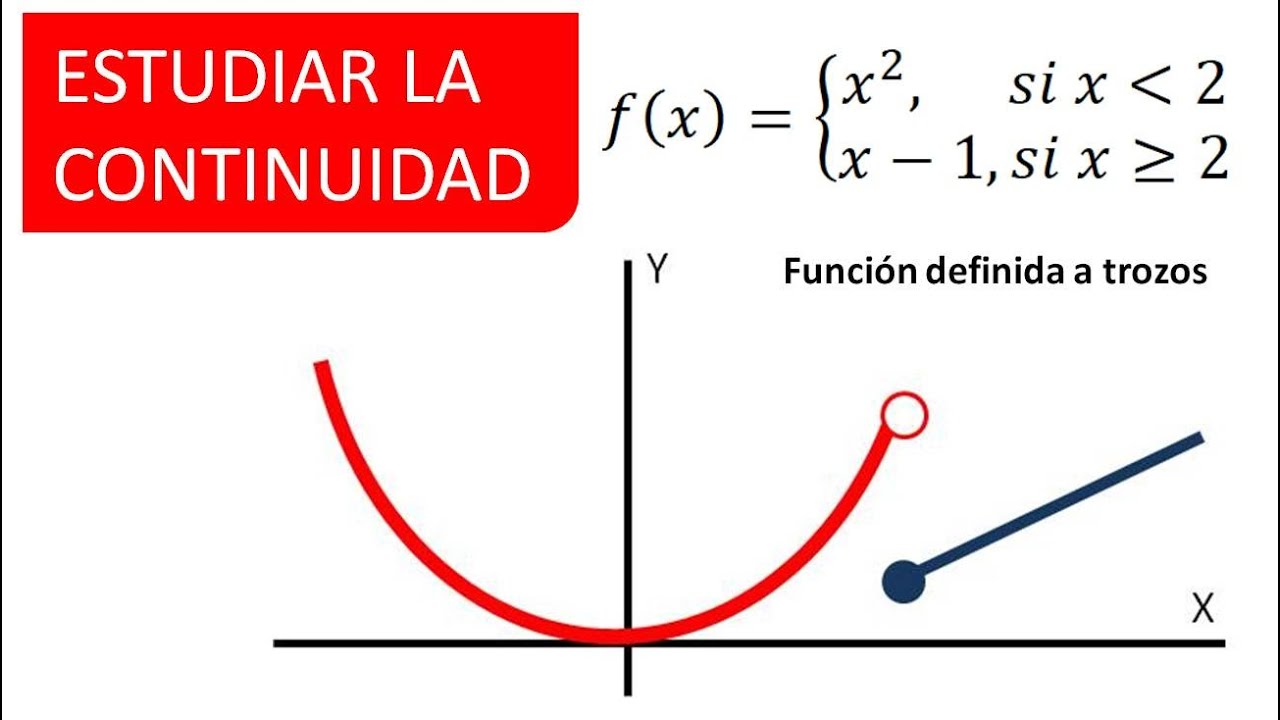
ESTUDIO DE LA CONTINUIDAD. FUNCIÓN DEFINIDA A TROZOS YouTube

Continuidad 4º ESO by Juanjo Expósito Issuu
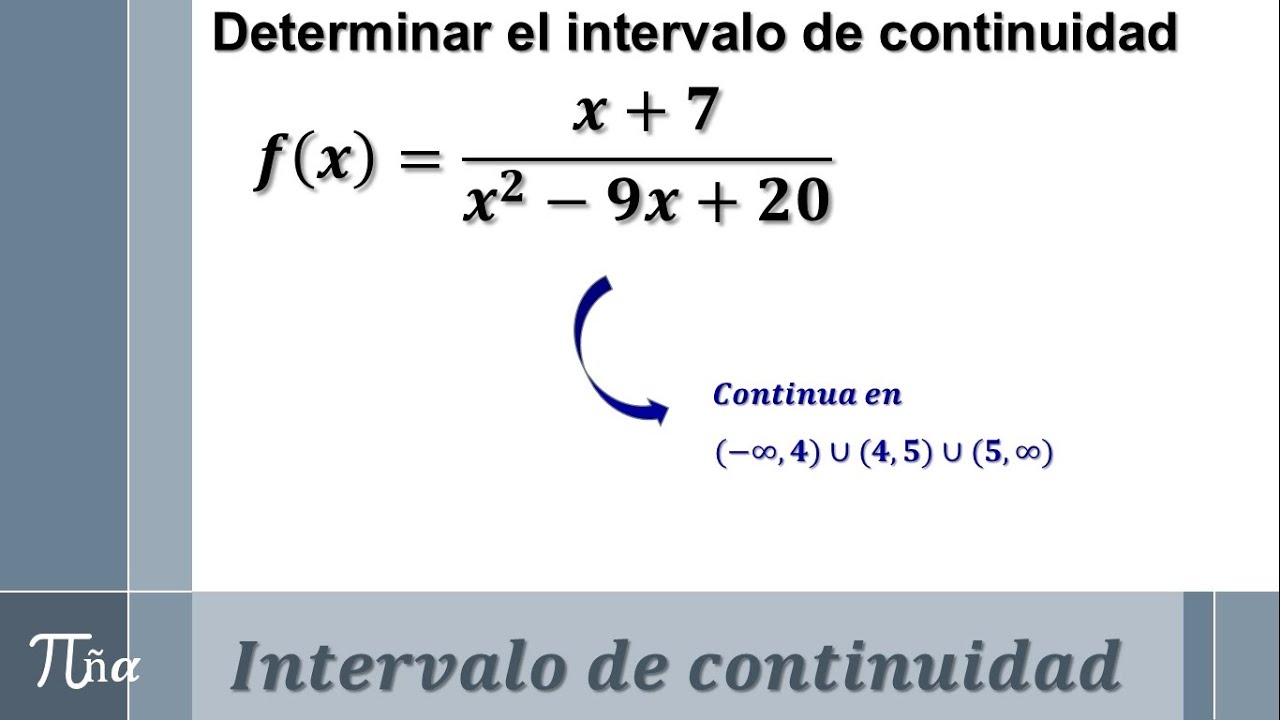
Intervalo de continuidad (ejemplo 4) YouTube

Cálculo Diferencial Continuidad 3 YouTube
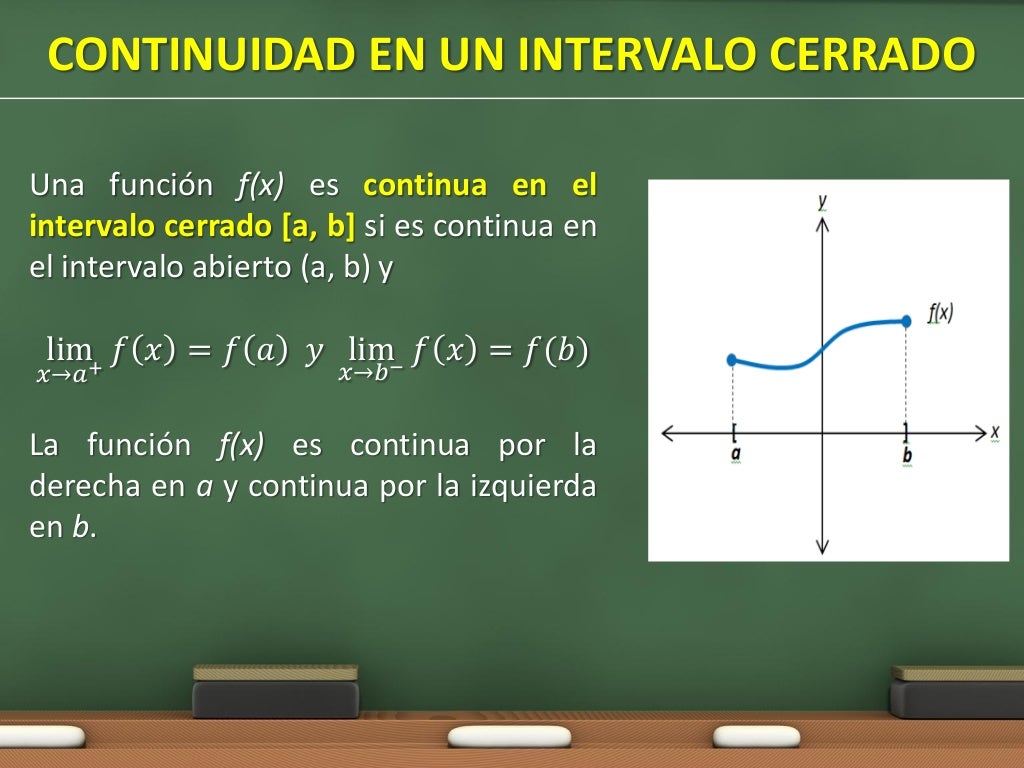
Continuidad (Cálculo I)

Puntos de discontinuidad e intervalo de continuidad en una gráfica (ejemplo 5) YouTube
La continuidad es importante en matemáticas porque en una función continua, un pequeño incremento en ocasiona un pequeño incremento en . No así con las funciones discontinuas. En otras palabras, para una función continua, cuando tiende a cero, tiende a , independientemente de que nos acerquemos a por la derecha o por la izquierda.. El límite y el valor de la función coinciden: Se dice que una función es continua en un intervalo si es continua en todos sus puntos. Si f (x1)= y1, la continuidad en x1 se expresa así: parafraseando, cuando x se aproxima a x1, f (x) se aproxima a y1. Por definición de los límites, esto significa que para todo intervalo abierto J.